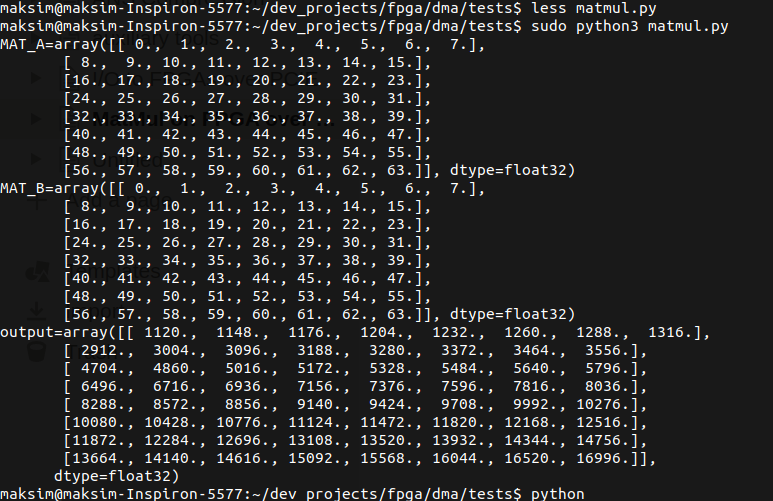
Working with MLIR
Random tips on working with the MLIR (LLVM) (and, possibly, other large C++ codebases).
These are in no particular order1. Skim (don’t peruse) and come back and use ctrl+f.
-
I am updating this as they occur to me (and adding/prepending at the top). ↩