• Normal random variable
• Footnotes

This post follows this video and covers change of measure for a single Normal random variable.

Normal random variable

Assume $ X \sim N(0,1)$ is distributed standard Normal. Recall the density $p(x)$ for the standard Normal

\[p(x) = \frac{1}{\sqrt{2\pi}} e^{-\tfrac{1}{2} x^2}\]

and that the cumulative distribution function (CDF)

\[P\left( X \leq x\right) = \int\limits_{-\infty}^x p(t)dt\]

or in differential form

\[dP(x) = p(x) dx\]

The differential form makes clear that the CDF is a probability measure insofar as it is positive, assigns numbers between 0 and 1 to events (sets), and sub-additive (left as exercise to the reader :) For example the probability that $X$ is in the interval $A=[\alpha, \beta]$, i.e. between $\alpha$ and $\beta$

\[P\left(\alpha \leq X \leq \beta\right) = \frac{1}{\sqrt{2\pi}}\int\limits_{\alpha}^{\beta} e^{-\tfrac{1}{2} x^2} dx\]

Therefore a change of CDF is tantamount to a change of measure. For example let’s shift the interval over which we’re computing $P$ by $\mu$ (i.e. to the right by $\mu$):

\[P\left(\alpha-\mu \leq X \leq \beta-\mu\right) = \frac{1}{\sqrt{2\pi}}\int\limits_{\alpha-\mu}^{\beta-\mu} e^{-\tfrac{1}{2} x^2} dx\]

We can reason about how such a shift affects the density; we perform the change of variables $Y = X + \mu$

\[P\left(\alpha-\mu \leq X \leq \beta-\mu\right) = \frac{1}{\sqrt{2\pi}}\int\limits_{\alpha}^{\beta} e^{-\tfrac{1}{2} (y-\mu)^2} dy\]

and changing the dummy variable $y$ back to $x$ (and expanding the square)

\[\begin{align} P\left(\alpha -\mu \leq X \leq \beta-\mu\right) &= \frac{1}{\sqrt{2\pi}}\int\limits_{\alpha}^{\beta} e^{ -\tfrac{1}{2} x^2 } e^{ x\mu-\tfrac{1}{2}\mu^2 } dx \\ &= \int\limits_{\alpha}^{\beta} e^{x\mu-\tfrac{1}{2}\mu^2} p(x)dx \\ &= \int\limits_{\alpha}^{\beta} e^{x\mu-\tfrac{1}{2}\mu^2} dP(x) \\ &= \int\limits_{A} e^{x\mu-\tfrac{1}{2}\mu^2} dP(x) \\ &= \int\limits_{-\infty}^{\infty} e^{x\mu-\tfrac{1}{2}\mu^2} 1_{A} dP(x) \\ &= E^P \left[e^{X\mu-\tfrac{1}{2}\mu^2} 1_{A} \right] \end{align}\]

Denoting the random variable $ Z(X) = e^{X\mu-\tfrac{1}{2}\mu^2} $ we can rewrite the last line as

\[P\left(\alpha -\mu \leq X \leq \beta-\mu\right) = E^P \left[Z(X) 1_{A} \right]\]

where the last line is pronounced “the expectation of $Z(X)$ under the measure $P$”. We can use this change in the integrand to define a new measure. Define $Q$ to be a new CDF

\[\begin{aligned} Q(X \leq a) &= E^P \left[e^{X\mu-\tfrac{1}{2}\mu^2} 1_{X \leq a} \right] \\ &= \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{\infty} e^{ -\tfrac{1}{2} x^2 } e^{ x\mu-\tfrac{1}{2}\mu^2 } 1_{x\leq a} dx \\ &= \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{a} e^{ -\tfrac{1}{2} x^2 } e^{ x\mu-\tfrac{1}{2}\mu^2 } dx \\ &= \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{a} e^{ -\tfrac{1}{2} (-2x\mu + \mu^2 +x^2)} \\ &= \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{a} e^{ -\tfrac{1}{2} ( x-\mu )^2} \\ \end{aligned}\]

which shows that $Q$ is just the CDF of a mean shifted Normal $N(\mu, 1)$ and therefore a probability measure.

To see what’s happening concretely consider this concrete example

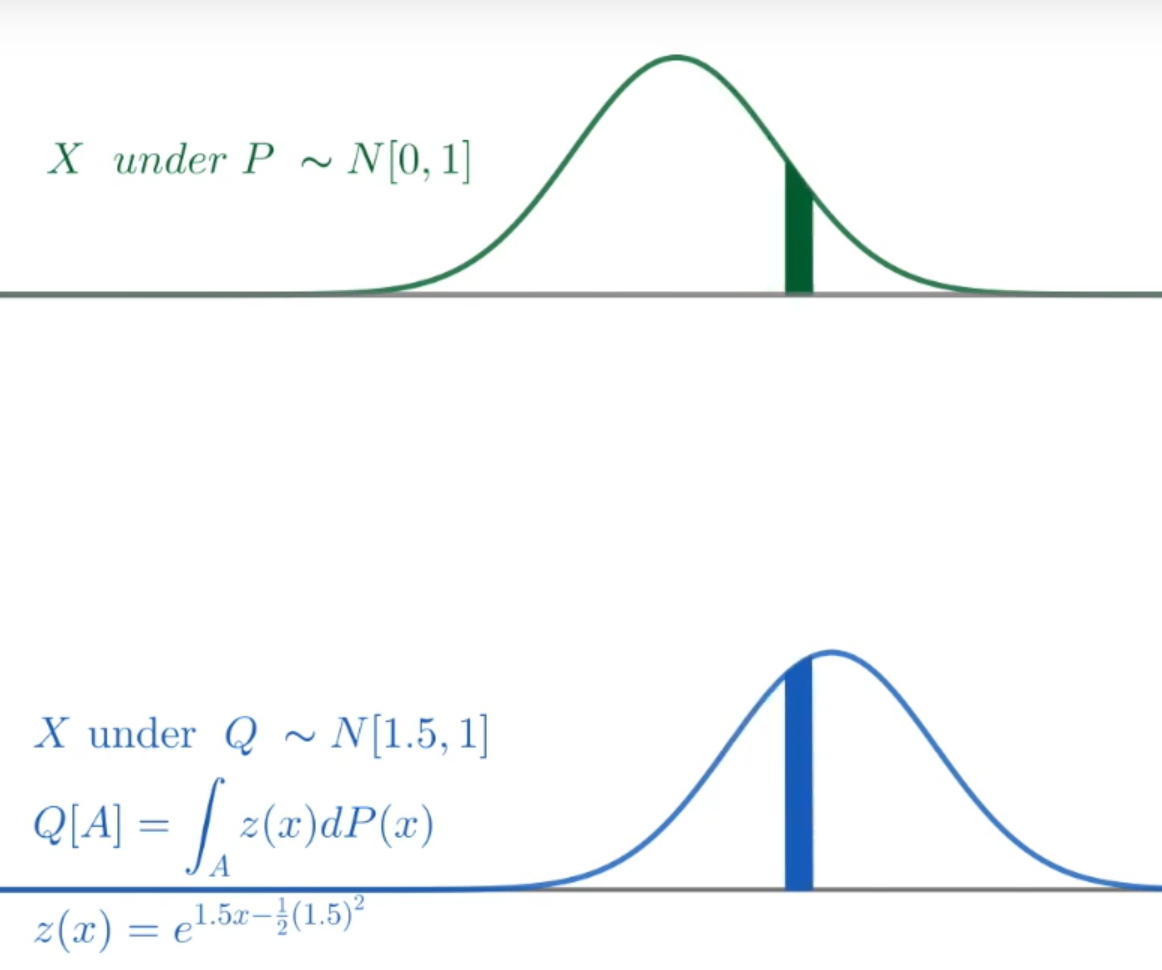
Note how the probability of an interval at the tail increases under the change of measure (blue interval vs. green interval).

This demonstrates that starting with a probability measure $P$ and shifting the interval of integration induces a new probability measure $Q$. Indeed there is a precise relationship between the two measures

\[\begin{align} Q(\alpha \leq X \leq y) &= \int\limits_\alpha^y e^{x\mu-\tfrac{1}{2}\mu^2} dP(x) \\ Q(y) - Q(\alpha) &= \int\limits_\alpha^y z(x) dP(x) \end{align}\]

where $z(x)$ is the density of $Z(X)$.

This is subject absolute continuity constraints on $Q$: a function $F(y)$ is absolutely continuous w.r.t. $y$ on $[a,b]$ if for every $\varepsilon > 0$, there is a $\delta$ such that

\[\sum_{i=1}^{n} |b_i - a_i| < \delta \implies \sum_{i=1}^n |F(b_i)-F(a_i)| < \varepsilon\]

for all partitions $\Pi := \left \{ (a_1, b_1), (a_2, b_2), \dots, (a_n,b_n) \right \}$ of $[a,b]$. For general measures $Q,P$ the Radon-Nikodym theorem states that if $Q \ll P$¹ then

\[\frac{dQ(x)}{dP(x)} = z(x)\]

where $z(x)$ is called the Radon-Nikodym derivative of $Q$ w.r.t. $P$. We have proven that $Q$ is a measure but not that it is a probability measure². We omit this proof. We summarize properties of the expectation under change of measure

\[E^P \left[ Z(X) h(X)\right] = \int\limits_{-\infty}^{\infty} \frac{dQ(x)}{dP(x)} h(x) dP(x) = \int\limits_{-\infty}^{\infty} h(x) dQ(x) = E^Q \left[ h(X)\right]\]

Footnotes