Complete search
August 22, 2018
Generating subsets
Alternatively choose to include and not include element from array and branch (making sure to undo the last move after both branches).
def all_subsets(A):
n = len(A)
subset = []
def search(k):
if k == n:
print(subset)
else:
# don't push
search(k+1)
subset.append(A[k])
search(k+1)
# undo push
subset.pop()
search(0)
Generating permutations
Given a substring that is the last permutation (lexically last) change that string the least; i.e. swap the next character into the smallest place it can go and then reverse the string.
def next_perm(A):
n = len(A)
# find longest tail weakly decreasing
i = n - 1
while i-1 > 0 and A[i-1] >= A[i] :
i -= 1
# A[i-1] < A[i]
j = i-1
while i < n and A[j] <= A[i]:
i += 1
# A[j] > A[i] so swap
A[j], A[i-1] = A[i-1], A[j]
# now reverse
return A[:j+1] + reversed(A[j+1:])
N Queens
Place $n$ queens on an $n \times n$ chessboard without any attacking any of the others.
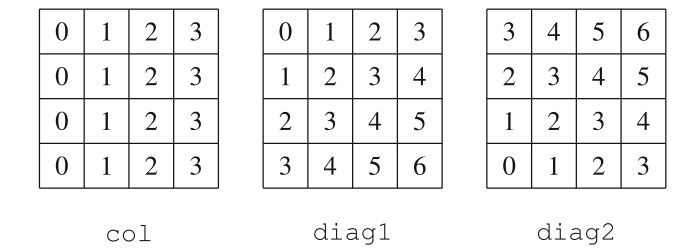
Knowing which diagonal you’re is the only tricky part. To figure it out flip the diag1 and diag2 grids and compute
manhattan distance from the 0 (this will give the lines of equidistance i.e. diagonals in manhattan metric).
def nqueens(n):
column = n*[0]
diag1 = (2*n-1)*[0]
diag2 = (2*n-1)*[0]
count = 0
def search(y):
if y == n:
count += 1
return
# iterate over the columns to look for a potential position
for x in range(n):
# (x,y) is on antidiagonal x+y and diagonal (n-1-y+x)
if column[x] or diag1[x+y] or diag2[n-1-y+x]: continue
column[x] = diag1[x+y] = diag2[n-1-y+x] = 1
search(y+1)
column[x] = diag1[x+y] = diag2[n-1-y+x] = 0
