Counting and Radix sort
August 20, 2018
Two sorts that beat $ O \left(n\log n\right) $ complexity.
Counting sort
Just count how many of each integer between min and max appear in the array.
from collections import OrderedDict
def counting_sort(array):
mmin, mmax = min(array), max(array)
counts = OrderedDict([])
for i in range(mmin, mmax):
counts[i] = 0
for a in array:
counts[a] += 1
sorted_array = []
for i,c in counts.items():
if c > 0: sorted_array.extend(c*[i])
return sorted_array
Radix sort
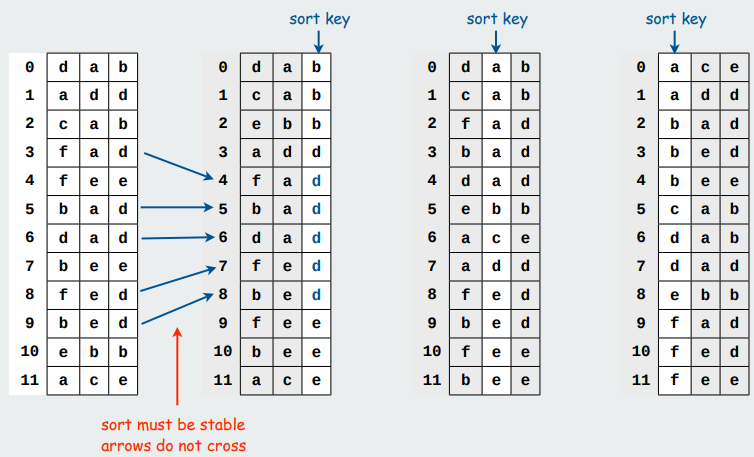
Sort in a stable fashion by column
def radix_sort(nums, base=10):
def to_buckets(nums, base, column):
buckets = [[] for x in range(base)]
for n in nums:
digit = (n // base ** column) % base
# 132 // 10 = 13; 13 % 10 = 3
buckets[digit].append(number)
def to_list(buckets):
numbers = []
for b in buckets:
for n in b:
numbers.append(n)
maxval = max(nums)
i = 0
while base ** i <= maxval:
sorted_nums = to_list(
to_buckets(nums, base, i)
)
return sorted_nums
Complexity is clearly $ O\left(kn \right) $ where $k$ is “word width” and $n$ is the length of the array.